Hyperelastic Material Models in Abaqus. When to Choose What?

To model the behaviour of rubbers and rubber-like materials, typically hyperelastic material models are used. A hyperelastic material is elastic: after unloading, the material returns to its original shape. The material state therefore does not depend on the history or the rate of deformation, but only on the current loading. The model is based on a strain energy potential, which is a function of the (invariants of the) current strain.

A hyperelastic material model is also non-linear: large strains can be applied, and the relationship between stress and strain is not a straight line.

The material models are formulated in such a way that they allow incompressibility: the volume of the material stays (almost) constant under loading. Because of this, a tension in one direction will lead to a large compression in the other directions. Therefore large differences between the engineering stress (force divided by initial area) and the true stress (force divided by the current area) can occur.

Rate-dependent: Viscoelasticity

Often, rubbers aren’t completely elastic: there is a rate dependent effect as well. If the material is tested and simulated at the same rate, it may not be necessary to include this. Only including hyperelastic properties may suffice in this case. If the rate-dependent effects are important, viscoelasticity can be included. Then the combined material behaviour does depend on the history. In Abaqus, the hyperelastic and viscoelastic behaviour are defined separately. The hyperelastic behaviour is provided as either instantaneous or long-term properties. Instantaneous properties are those at t=0, when the material has not have had the time to relax at all. Long-term properties are those at t=infinite, when the material is fully relaxed. In the rest of the blog we will focus on the elastic properties. An example of a rubber part including viscoelasticity is given in this blog.

Figure 1: example of the influence of including viscoelasticity: the stress reduces in time.

Making a Fit: Material Evaluation

To describe the hyperelastic material behaviour, typically material data is used. Often test data from a uniaxial test is available. In some cases more data is available or needs to be obtained. Within Abaqus, it is possible to make a material fit for different material models and let Abaqus determine the material constants that match the data best. This is a straightforward process with visual feedback showing how well the fitted data matches the experimental data for different models. It is explained in more detail in this blog.

Figure 2: Example of results from material evaluation.

This fit is made, by minimizing the least squares error for the points included. It is therefore important to ensure that the data points provided are under loading states of interest. If many points at small strain are included for example, then the fit will be most accurate in this strain region.  

Overview of Material Models Available

The hyperelastic material models available in Abaqus are Arruda-Boyce, Marlow, Ogden, Polynomial and Van der Waals. Special cases of the Polynomial model are also available directly. These include the Mooney-Rivlin and reduced polynomial forms. Special cases of the reduced polynomial form are also available: the Neo-Hookean and Yeoh models.

In the table below, all available models are listed, as well as the number of parameters included in the model.

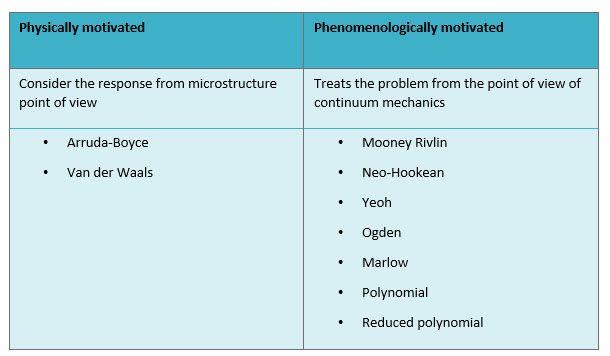
Physically Vs Phenomenologically Motivated

The hyperelastic material models available in Abaqus can be categorized as either physically motivated or phenomenologically motivated. Models that are physically motivated, consider the response of the material from a microstructural point of view. This is the case for the Arruda-Boyce model and the Van der Waals model. They have a sound background and are expected to provide reasonable material behaviour under different load states if a fit can be made.

The phenomenologically motivated models treat the problem from a continuum point of view, they are used simply because they work reasonably well and are typically not overly complex.

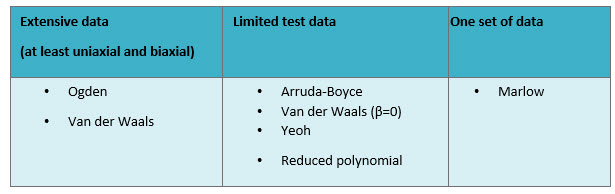
Recommended Models Based on Amount of Available Data

A complex model with many parameters may be able to describe data better because there are more options. However, if you try to fit many parameters when only limited data is available, there may be multiple parameter sets with similarly accurate fits compared to the available data, but a different response in not tested cases. The chance of obtaining an unstable model is also higher with more complex models. It is therefore recommended to use more extensive models when more data is available, and a relatively simple model when limited data is available. Using a model including the second invariant of the strain (polynomial, Mooney-Rivlin) can be troublesome in any case.

An overview of recommended material models depending on the amount of test data available is given in the table below:

Marlow Model

The Marlow model is a special case because it does not require parameters to be fit (like the other models do). Instead, only one set of test data is provided (e.g uniaxial tension), and the model follows the provided data exactly. It usually provides reasonable results in the other directions as well. For 3D data, either tension or compression data can be used. If the entire range from compression to tension is specified, you need to decide which data will be used. For beams it is possible to use both at the same time. If limited data is available, then this is usually a good first choice.

Material Model Stability

In implicit non-linear analyses, convergence of the Newton-Raphson scheme is required. This is based on the stiffness and can be difficult or impossible if the stiffness is negative: if the stress reduces while the strain increases. When performing a material evaluation, Abaqus provides stability information as mentioned here. Some models are always stable under certain conditions:

• Arruda-Boyce for positive values of the initial shear modulus and locking stretch
• Neo-Hookean for a positive coefficient C10
• Yeoh model if all coefficients Ci0 >0: if C20 is less negative or C10 is more positive, stability will increase.

Volumetric Data

Rubbers tend to be approximately incompressible. If the material is unconfined, then assuming (approximate) incompressibility may suffice. If the material is confined, then the volumetric behaviour becomes important, and this should be tested and included in the model as well.

Conclusion

In conclusion, Abaqus offers many material models to describe rubber-like behaviour, including hyperelasticity and viscoelasticity.