Modelling loads of steady current and waves with Abaqus Aqua

Offshore structures are often loaded due to water and wind. The loads on the structure may vary in time and with position. It is possible to specify such loads in Abaqus directly. When applying these types of loads to beams, it may be easier to use Abaqus/Aqua.
Within Abaqus/Aqua the environment of a structure can be defined including a steady current, waves and a wind profile. Based on this environment, loads due to drag, buoyancy and inertia can be defined.
The Abaqus/Aqua options are not available from the CAE. In this blog, I will show how to define a current and Airy waves and apply a drag load based on this using the keyword editor.

The challenge

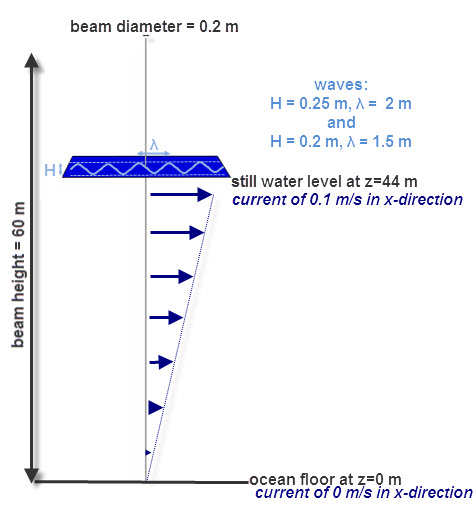
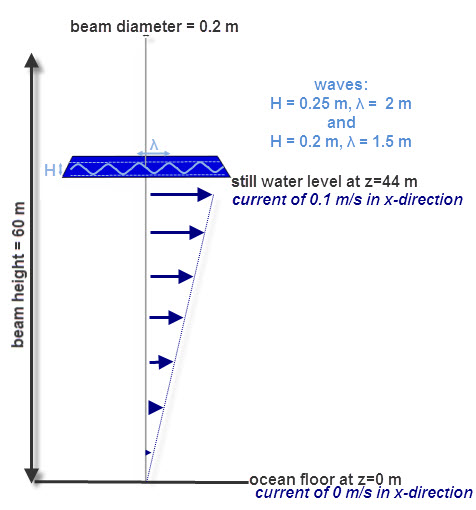
As example a circular beam with a diameter of 0.2 m and a length of 60 m is simulated. It is fixed to the ground and partially under water; the still water level is at 44 m. A current is specified in x-direction with a velocity of 0 at the ocean floor which increases linearly with height to 0.1 m/s at 44 m. Two sets of Airy waves are defined. One has a height of 0.25 m and a wavelength of 2 m. It travels in the x-direction. The other has a height of 0.2 m, a wavelength of 1.5 m and it travels at an angle of 45 degrees with respect to the x-axis in the x-y plane.

Model Set-Up

The basic model set-up is similar to what it would be without Abaqus/Aqua:

A part is defined for the beam. This must be a wire, to allow Abaqus/Aqua loads to be calculated. A material model, profile and section are created and assigned. The part is instanced into the assembly and oriented in such a way the z-direction corresponds to the vertical direction. This is assumed by Abaqus/Aqua for 3D simulations; for 2D simulations the y-direction should correspond to the vertical direction. A step is created and appropriate boundary conditions are applied.

To visualise the waves, a shell part is created besides the beam. A mesh of surface elements are used for this part, and no properties are assigned to it. It is placed in such a way that is forms the still water surface, so horizontally at the still water height.

Defining offshore environment: current and waves

Once the main model is set up, the offshore environment can be defined. This is done via keywords. By clicking model > edit keywords and selecting the model for which the keywords should be edited, it is possible to modify keywords in the input file from Abaqus/CAE. These are stored in the .cae file. This avoids manually having to modify an input file repeatedly.

The environment is defined using the *AQUA keyword. As can be checked in the Abaqus Keywords Reference Guide, the keyword should be placed at the model level (for example just before the step definition) and the syntax is as follows:

*AQUA
Elevation of the seabed, elevation of the still fluid surface, gravitational constant, mass density of the fluid

Steady velocity of the fluid in the X-direction, steady velocity of the fluid in the Y-direction, Steady velocity of the fluid in the Z-direction (only relevant for 3D cases), elevation, X-coordinate defining the location where the velocity applies (if this value is omitted the velocity is assumed to be independent of X-direction), Y-coordinate defining the location where the velocity applies (only relevant for 3D; if omitted, velocity is assumed to be independent of Y)

This last line can be repeated as often as required to define the velocity of the current at different positions.

So, for the specified problem, where the seabed is at z=0 and SI units are used, this leads to:

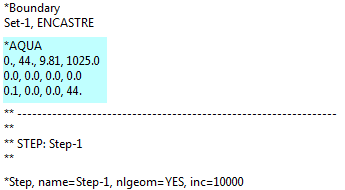
Note that the specified velocity is interpolated linearly between the points at which it is defined.

With this the current is defined, but the waves are not. This required the *WAVE keyword. For Airy waves (linear waves with small height compared to water depth) the syntax is as follows:

*WAVE, TYPE=AIRY
Wave component amplitude, wavelength of this component, phase angle of this component, x-direction cosine defining the direction of travel for this wave component, y-direction cosine defining the direction of travel for this wave component (not needed in 2D cases).

The last line can be repeated as often as necessary to define all wave trains. The direction cosine is the cosine of the angle between the vector corresponding to the direction of travel of the wave and the specified direction (x- or y-axis). In two-dimensional cases only one directional cosine is needed, where +1.0 indicates a wave travelling in the direction of increasing x, while -1.0 indicates a wave travelling in the direction of decreasing x.

For the specified example, this leads to:

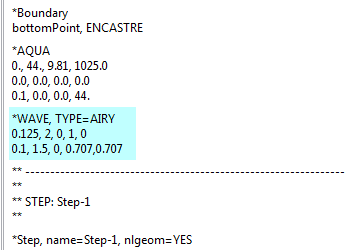
In this case, the phase angle is taken to be zero for both waves. The phase angle specifies the position of the wave at t=0. With a phase angle of zero, the waves are chosen such that they have a trough at the origin of the horizontal axis at t=0. A positive phase angle shifts the waves backwards in their travel direction, so for a wave travelling in positive x-direction, as small positive phase angle with provide a trough at a small negative x-value at t=0.

Defining load due to current and waves

Only specifying the current and waves, does not yet influence the simulation. It is necessary to define loads as well. In this case, transverse fluid drag loads are specified. Fluid drag loads are provided by Morison’s equation. The calculated force is only applied to portions of the structure immersed in the fluid. Using a similar approach to what was done here, wind and wind loading can be applied to the portions of the structure that are above the still fluid surface, but this is not discussed here. The load is applied using the *DLOAD option on the step level, with the following syntax:

*DLOAD
Element number or set, FDD, magnitude, effective outer diameter of the member, drag coefficient, structural velocity factor, amplitude for scaling current velocities, amplitude for wave velocities.

Here FDD specifies that it is a fluid drag load. The calculated force is multiplied by the specified magnitude and amplitude, as is common for other loads in Abaqus as well. The effective outer diameter can differ from the beam diameter, to take into account material providing drag, but not influencing structural properties. In this example, the effective outer diameter will be taken to match the diameter of the beam. The structural velocity factor defaults to 1, and this value is used in this simulation. This leads to:

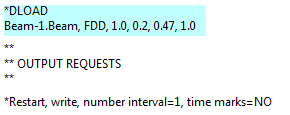
Requesting output for visualisation

With these settings, the simulation can be run and results for the beam can be obtained. If we want to see the waves applied, an additional step is necessary, namely requesting the visualisation of the waves using the previously created surface. This is done using *SURFACE SECTION, AQUAVISUALIZATION.

First an element set corresponding to all surface elements in the part is made on the part level. In this case, the set is named Set-1. The following syntax can then be used:

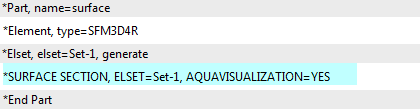
No loads or boundary conditions should be applied to the surface. If displacement output is requested for it, the deformation of the sea surface due to the waves will be visible in the .odb.

Results: reaction force in fully constrained model

To see the loads applied to the beam, it is completely fixed in all directions. Apart from the sign, the reaction forces then correspond to the applied force.

Results: stress and deformation in beam fixed to ocean floor

When only the bottom node is fully constrained, the beam can deform. Because it is stiff compared to the loading, the deformation is small. Exaggerating the deformation (300 x) and the beam thickness (30 times) shows the following stress and deformation:

Interested in discussing your challenge with us, to see if we can be of help with our FEA consulting services?