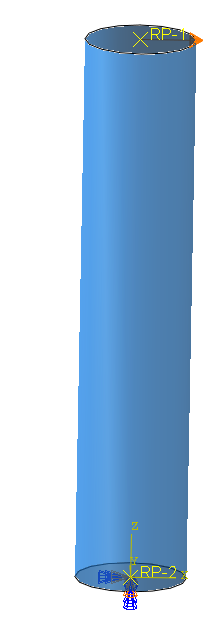Implicit Vs Explicit Finite Element Analysis: When to Use Which?

A fundamental question for each finite element problem is the type of solver to use: implicit or explicit? The solver type influences the set of equations that are solved, the availability of certain features, the run time and even whether a solution is obtained. It is therefore important. In this blog I’ll explain the difference between the two solvers available in Abaqus, their advantages and disadvantages, and when to choose which. I'll end with a simple example to illustrate the points made.

What Is the Difference?

When we talk about implicit or explicit in fea, we talk about the algorithm that is used for time incrementation. In both cases, the state of the model is calculated at multiple points in time and the new state is calculated based on the old state. With an explicit algorithm the new state can be calculated directly from the data available in the current state. It is basically an extrapolation. With an implicit algorithm the new state cannot be calculated directly from the old state; a coupled system of equations must be solved. This requires non-linear solution algorithms, typically the Newton-Raphson method.

Computational Cost and Time Increment Size

The computational cost of a single explicit increment is small; all information needed is available and the calculation is straight-forward and fast. However, the time increment cannot be too large, because then method becomes unstable and the error on the solution increases exponentially. This makes sense if we think of it as an extrapolation: extrapolating far beyond the known range tends to give wrong results, especially if errors have a chance to add up. The largest time increment that can be used is calculated automatically by Abaqus and it is referred to as the stable time increment. The stable time increment reduces with smaller element size, lower density, and higher stiffness. The element with the smallest stable time increment determines the time increment for the entire analysis; a single badly shaped element can therefore hugely impact the simulation time. The stable time increment is usually approximately constant throughout the analysis, so that the time required to run an analysis can be estimated once the first increments have completed.

The computational cost of an implicit increment is much larger, because a system of equations needs to be solved. For non-linear analysis, this even needs to be done multiple times. It will thus take more time and memory to solve a single implicit increment. The time increment size, on the other hand, is not limited by stability issues for implicit algorithm. This typically allows much larger time increments than for explicit algorithms. The increment size in Abaqus/Standard (the implicit solver) is usually determined automatically by Abaqus, based on how easily the Newton-Raphson scheme converges. This can vary significantly throughout the analysis. The more non-linear the problem is, the more computationally expensive it is to find a converged solution.

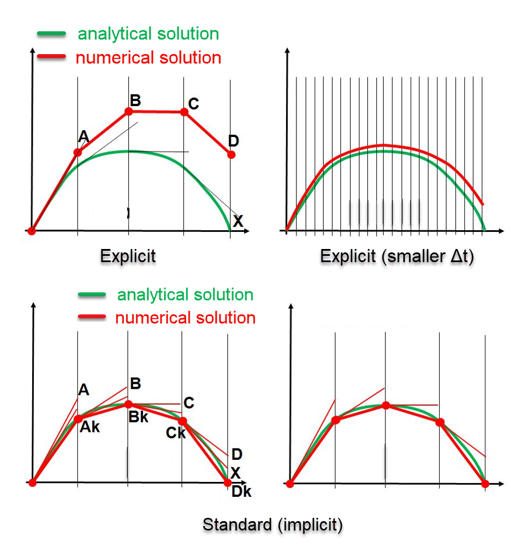
Figure 1: Time incrementation with explicit and implict (standard) solver. For explicit, larger time increments lead to larger errors on the solution (top row). For implicit, larger time increments do not lead to larger errors on the solution, due to the iterative approach used (Newton-Raphson method).

Choosing between Explicit and Implicit is therefore often choosing between many small increments and fewer larger increments.

Dynamic Effects

Abaqus/Standard, the implicit solver, can solve for static equilibrium: the state where the sum of the forces is zero. It is also possible to include dynamic effects. If dynamic effects are not included, a static equilibrium must exist. Inertia cannot be used to stabilize a system, so rigid body motions are not allowed: all parts need to be connected to the ground in all directions. Internal energy cannot be converted to kinetic energy in a static analysis. If this is needed to obtain equilibrium, then an implicit solver cannot find a solution without help, e.g. in the form of applying damping.

Abaqus/Explicit always calculates dynamic equilibrium: force = mass x acceleration. There are more vibrations in an Explicit analysis compared to a static implicit analysis, and results are more oscillatory. Time has a physical meaning, and the loading rate is of importance. The loading rate does not influence the stable time increment. A large amount of simulated time will therefore also take a large amount of simulation time. If dynamic effects are not of interest, the loading should be applied so slow that the force due to mass x acceleration does not play a role. This can be faster than the actual load application rate. An alternative to applying the load faster, is to increase the stable time increment by increasing the mass. This is termed mass scaling. Too much mass scaling will lead to unwanted dynamic effects.

Contact: Explicit Preferred

Contact can be included in both Abaqus/Standard and Abaqus/Explicit. It is not always defined in exactly the same way, but most options are available in both cases.

Changes in contact are extremely non-linear. Because of this, and implicit algorithm typically needs many iterations to resolve it. This is computationally expensive. Challenging contact problems are therefore often solved more easily in Abqus/Explicit.

Features Only Available in One Solver

Some options are only available in either Abaqus/Standard or Abaqus/Explicit. These include:

When to Use Which?

Abaqus/Standard is more beneficial for problems that are slow and relatively linear, while Abaqus/Explicit is more beneficial for problems that are fast and very non-linear.

Typically, most challenges arise for problems that are slow and extremely non-linear: should they be solved with Abaqus/Standard or Abaqus/Explicit? There isn’t always an easy answer to this question: Abaqus/Standard will give convergence issues, while Abaqus/Explicit will take long and/or give noisy results. Applying mass scaling may help to reduce the time needed in Explicit. It can be beneficial to first try Abaqus/Standard. If convergence is too troublesome, the implicit step can be replaced by an explicit step without having to set-up the entire model again.

The Best of Both Worlds

It is not possible to use both the implicit and the explicit solver in one analysis. It IS possible to first do an analysis with one solver, import the results, and continue from the state at the end of the first analysis in a second analysis that used a different solver. This is especially beneficial when combining mild preloading (implicit solver) with more extreme loading of interest (explicit) or when doing a forming analysis (explicit) and wanting to know the elastic spring back afterwards (implicit).

An Example

As an example, the bending of a cylinder is simulated. This simple example shows the advantages of standard and explicit.

The Set-up

A hollow steel cylinder (modelled with shell elements) is simulated (Figure 2). It is 500 mm long, has a diamter of 100 mm and a thickness of 0.5 mm. The top and bottom end are each connected to a reference point using a kinematic coupling. The bottom point is fully constrained, a displacement of 100 mm is applied to the top point.

Figure 2: The analysis set-up.

This is analysed using both Abaqus/Standard, and Abaqus/Explicit. In Abaqus/Standard, a step time of 1 s is used. In Abaqus/Explicit, either a step time of 1 s or a step time of 0.1 s is used. We will take a look at whether a solution is found, the time needed to obtain the solution, the deformed shape and the reaction force.

Results

The standard analysis does not complete: at around 12.5% of the step time, it stops due to convergence issues. The explit analyses do complete.The simulation times of the Standard analysis and the fast Explicit analysis (0.1s) are in the same order of magnitude. The simulation time for explicit with a step time of 1 (reference) is clearly larger, here we see that scaling the simulated time also scales the simulation time. For Abaqus/Standard there would be no difference if the simulated time is scaled.

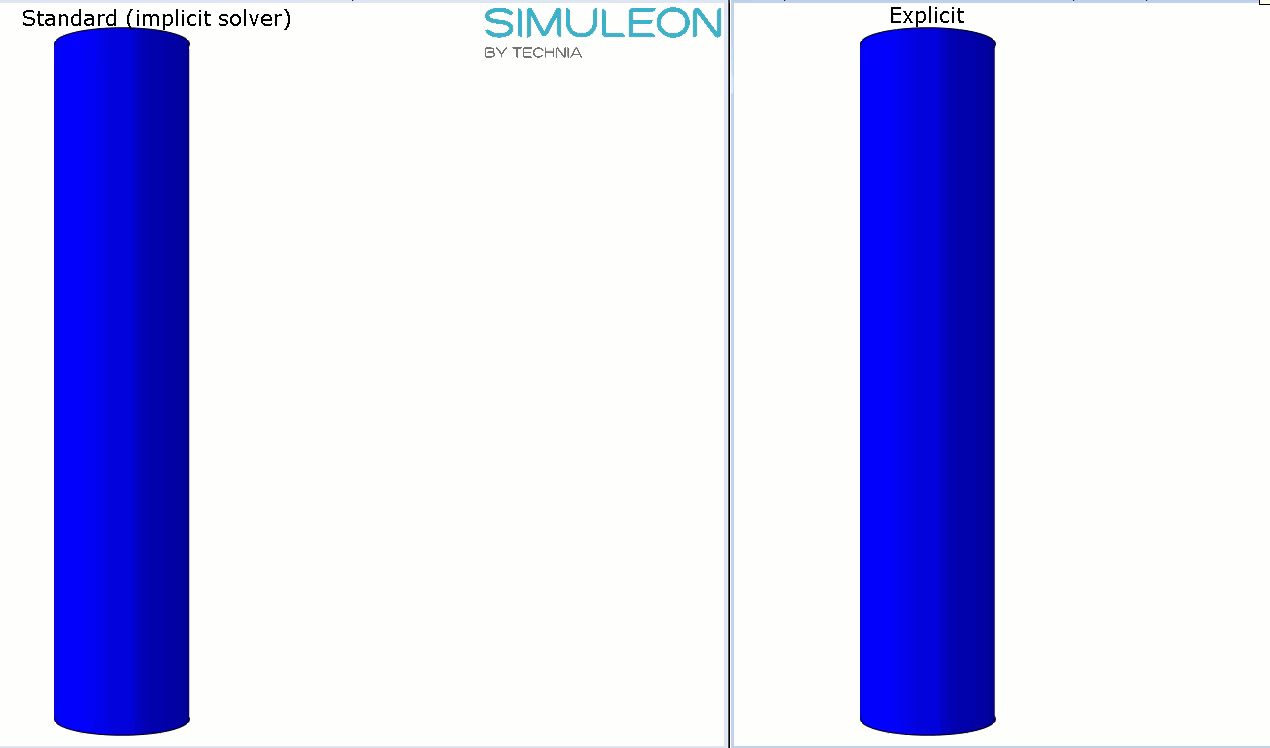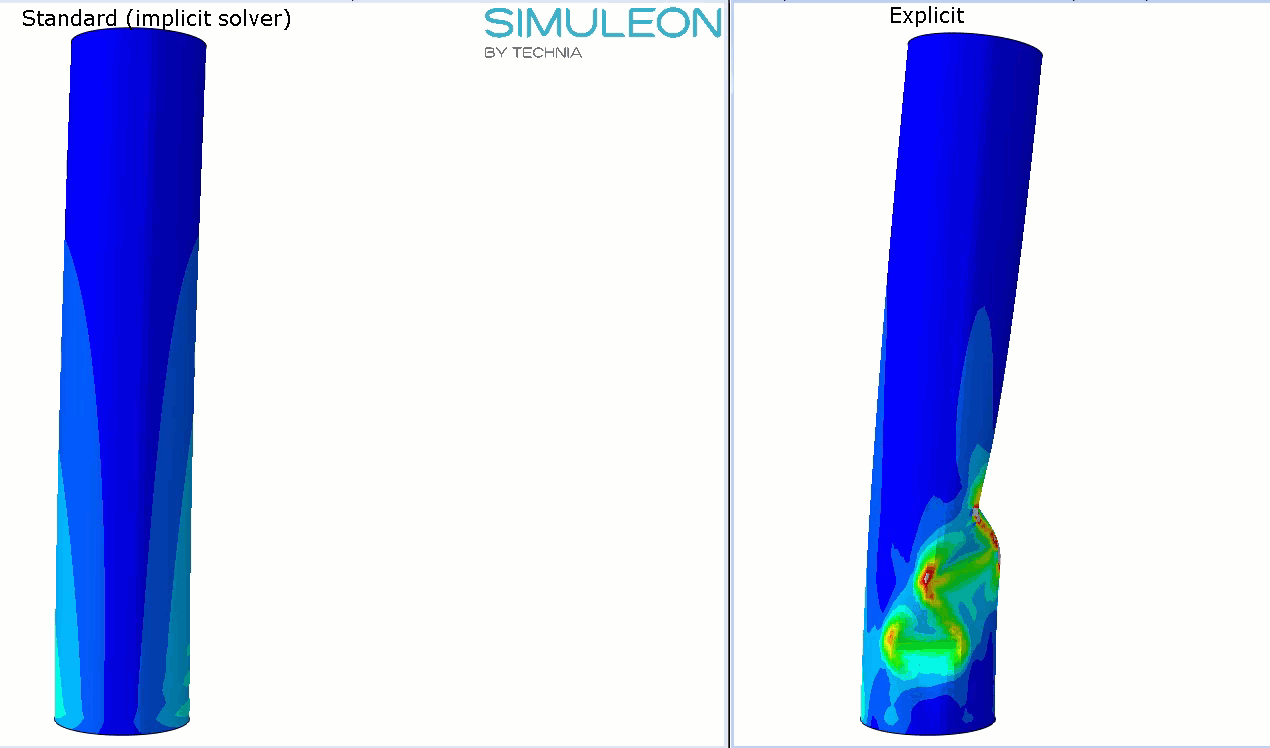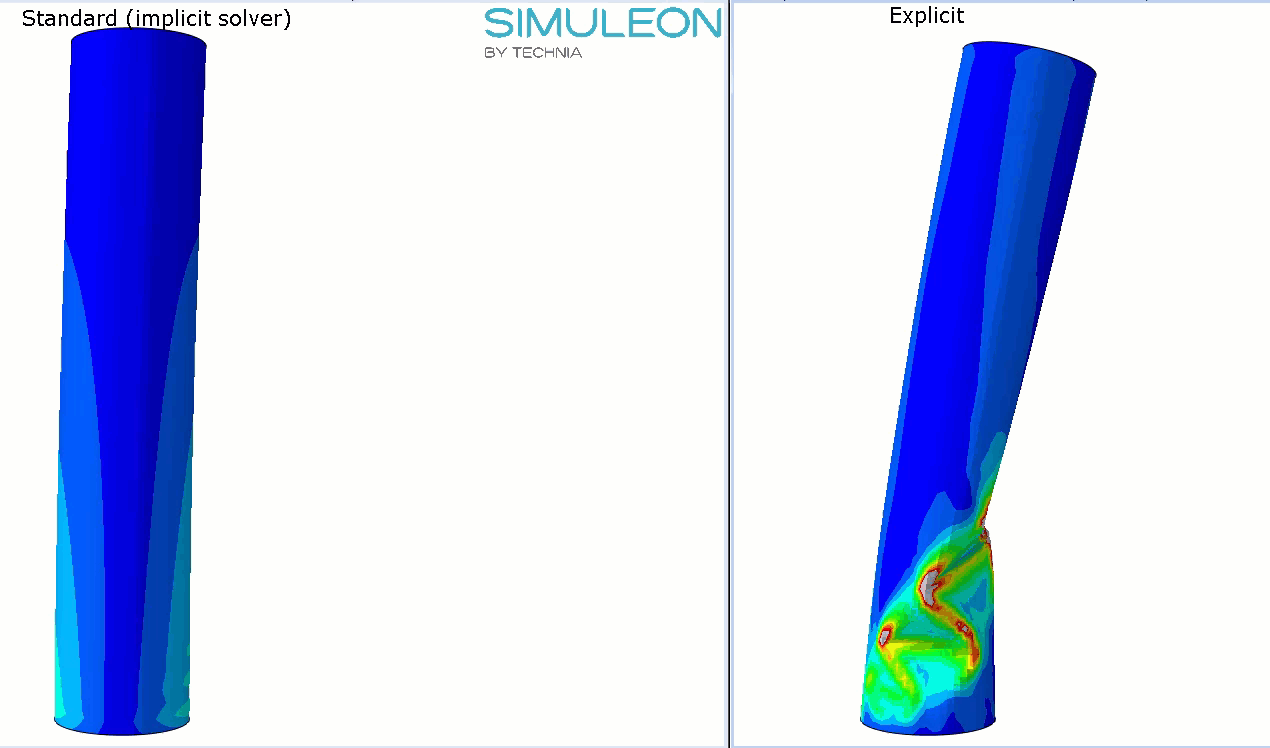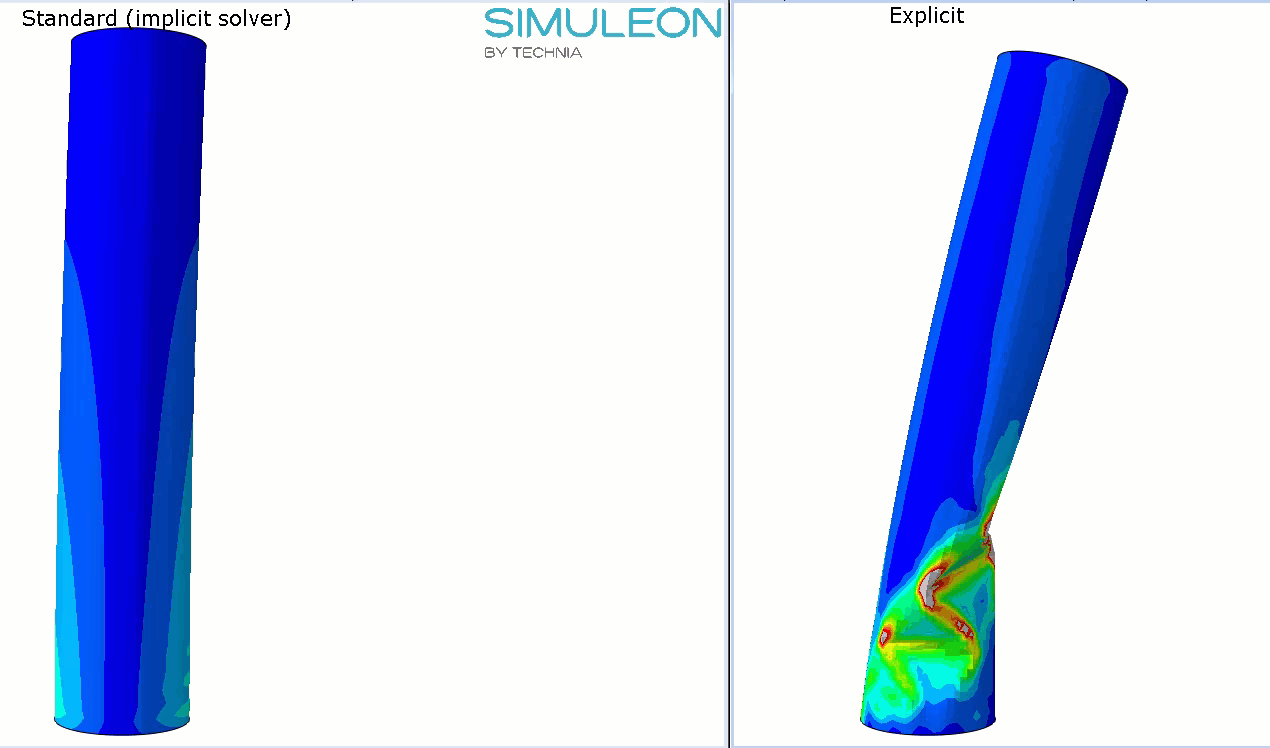
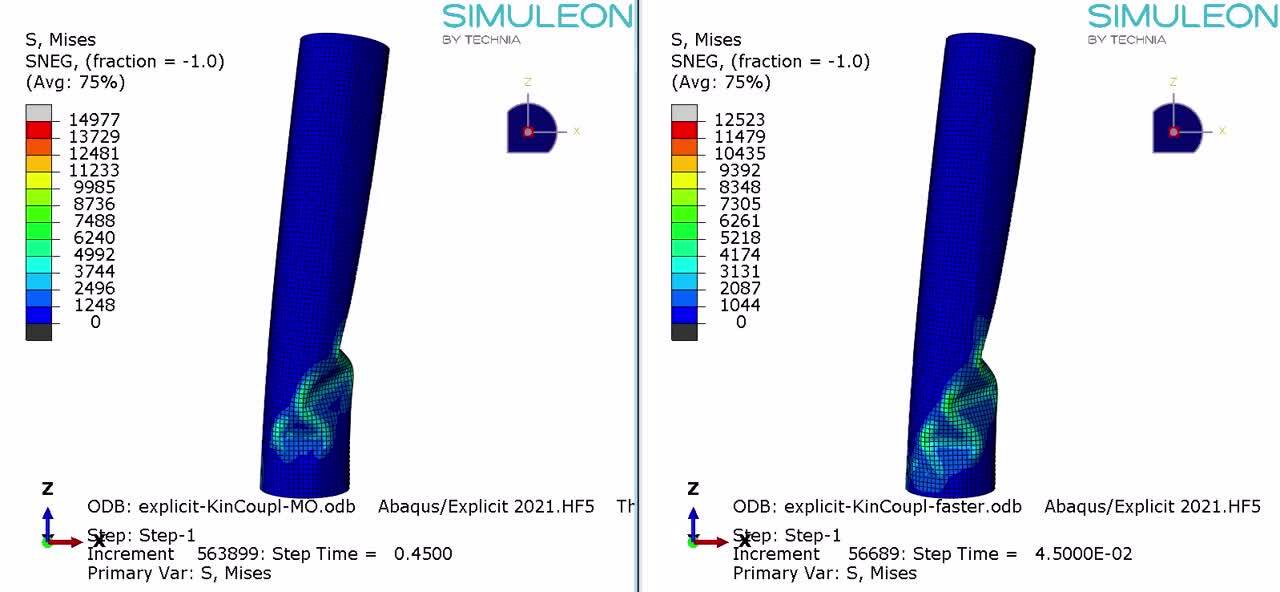
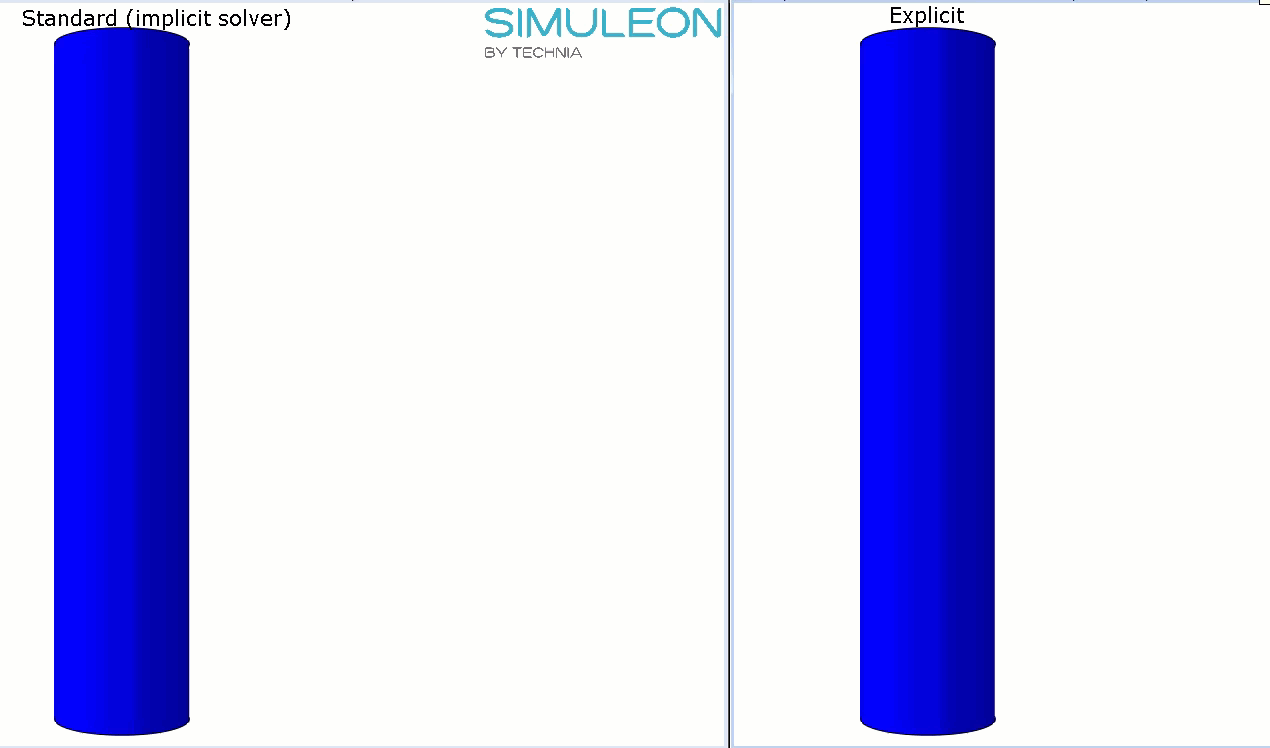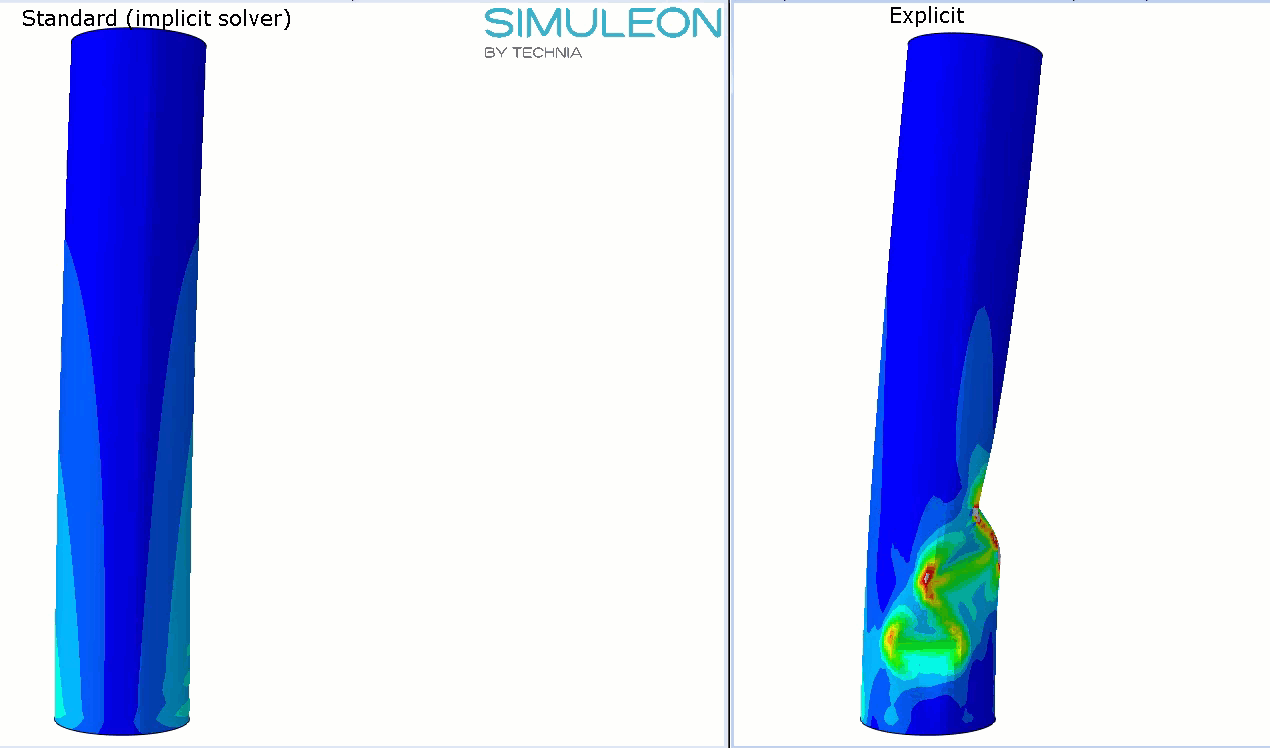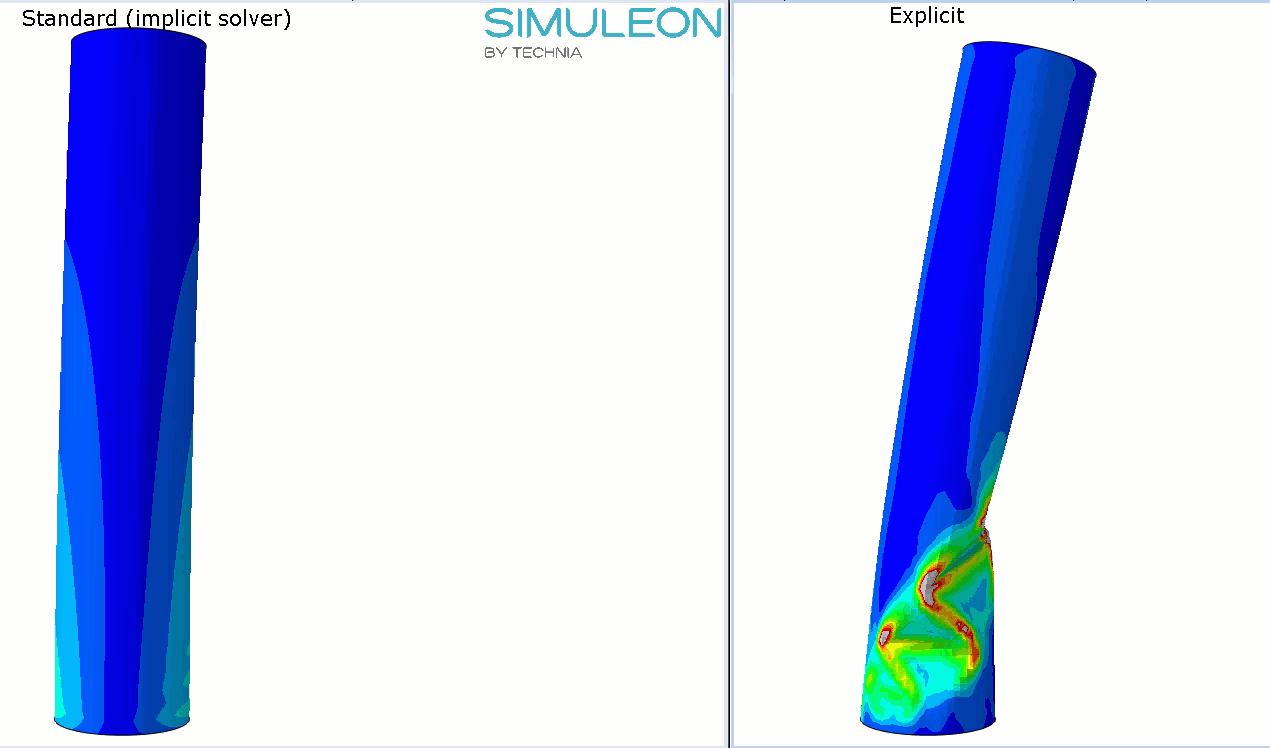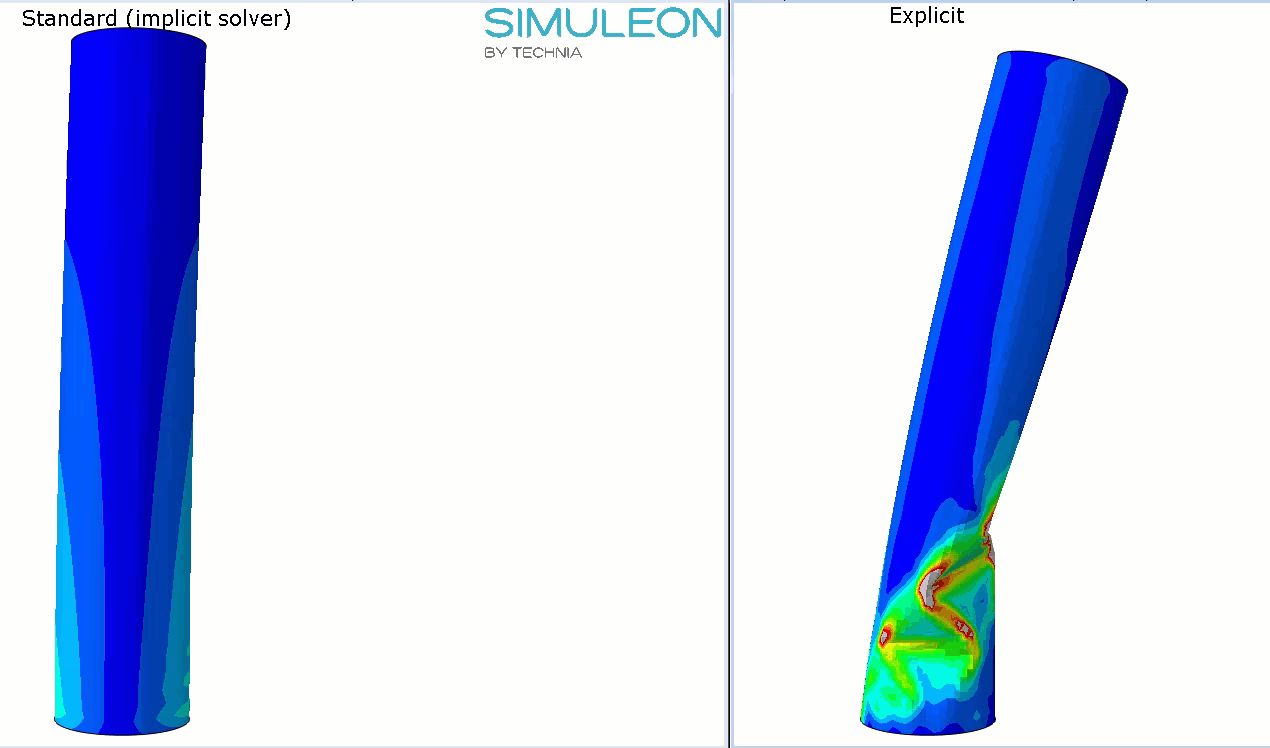
The deformed shape 10% of the total simulated time is similar in all cases:

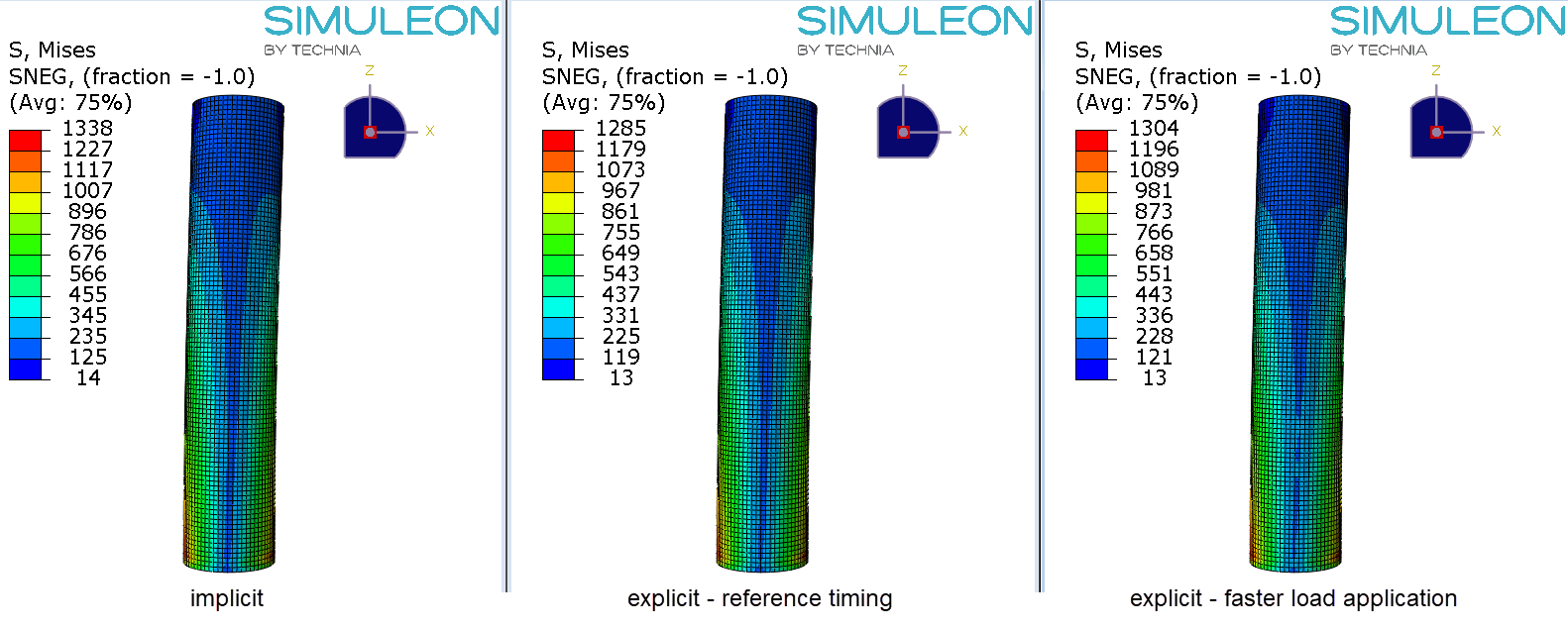
Figure 3: The deformed cylinder at around 10% of total applied loading for all three cases: implicit (left), explicit with reference timing (middle) and explicit with faster load application (right). Results are similar in all cases.

As the Explicit analyses continue, they both show buckling behaviour, though it is not exactly the same:

This buckling behaviour leads to convergence issues in the implicit analysis. Using Riks analysis may help here.

The average reaction force is similar in all cases (Figure 4). The reaction force is more oscilatory for the explicit analyses than for the standard analysis. Filtering is required to obtain reasonable values.

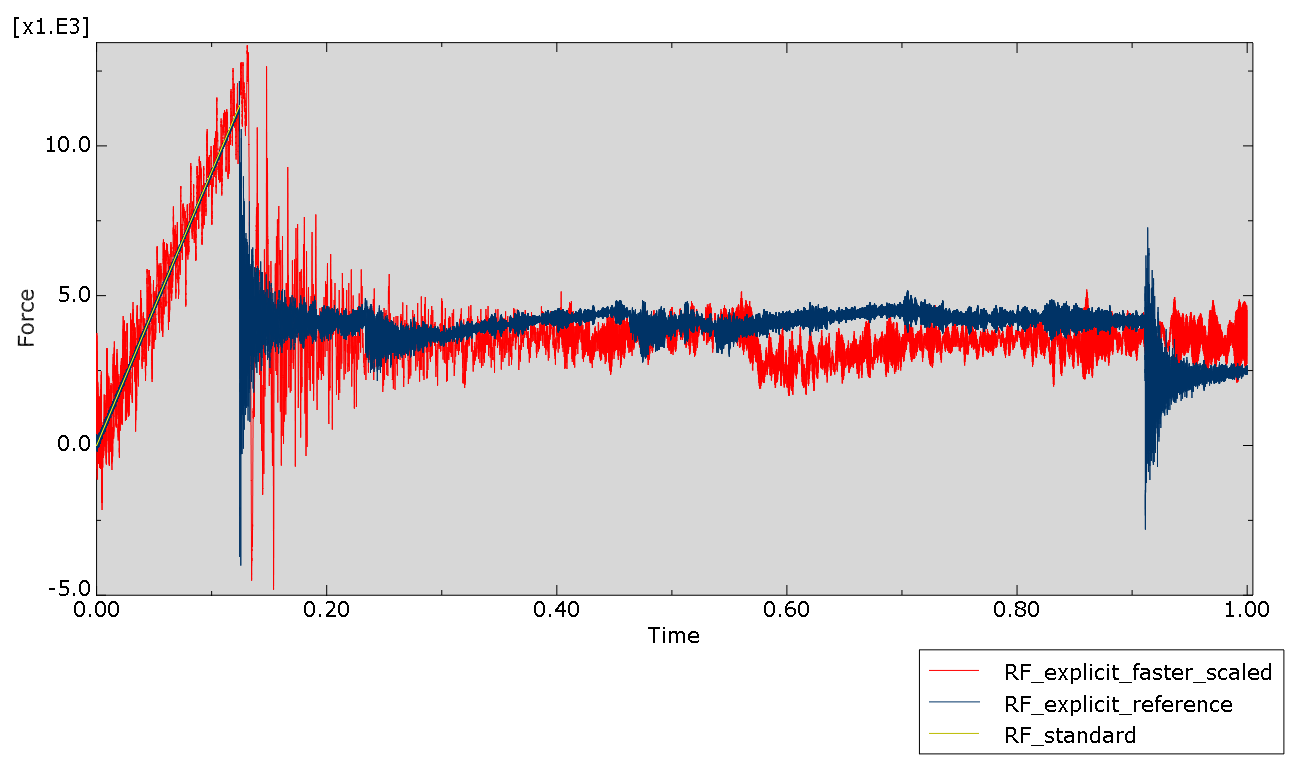
Figure 4: Reaction force for all cases tested. The blue line (explicit with reference timing) oscilates a lot less than the red line (explicit with faster load application). No oscillation is seen for the standard analysis (yellow dotted line). This curve stops at the maximal force observed in the other cases: it does not get past the buckling point.

The kinetic energy is larger when the load is applied faster (Figure 5).This is noticeable after the buckling point.

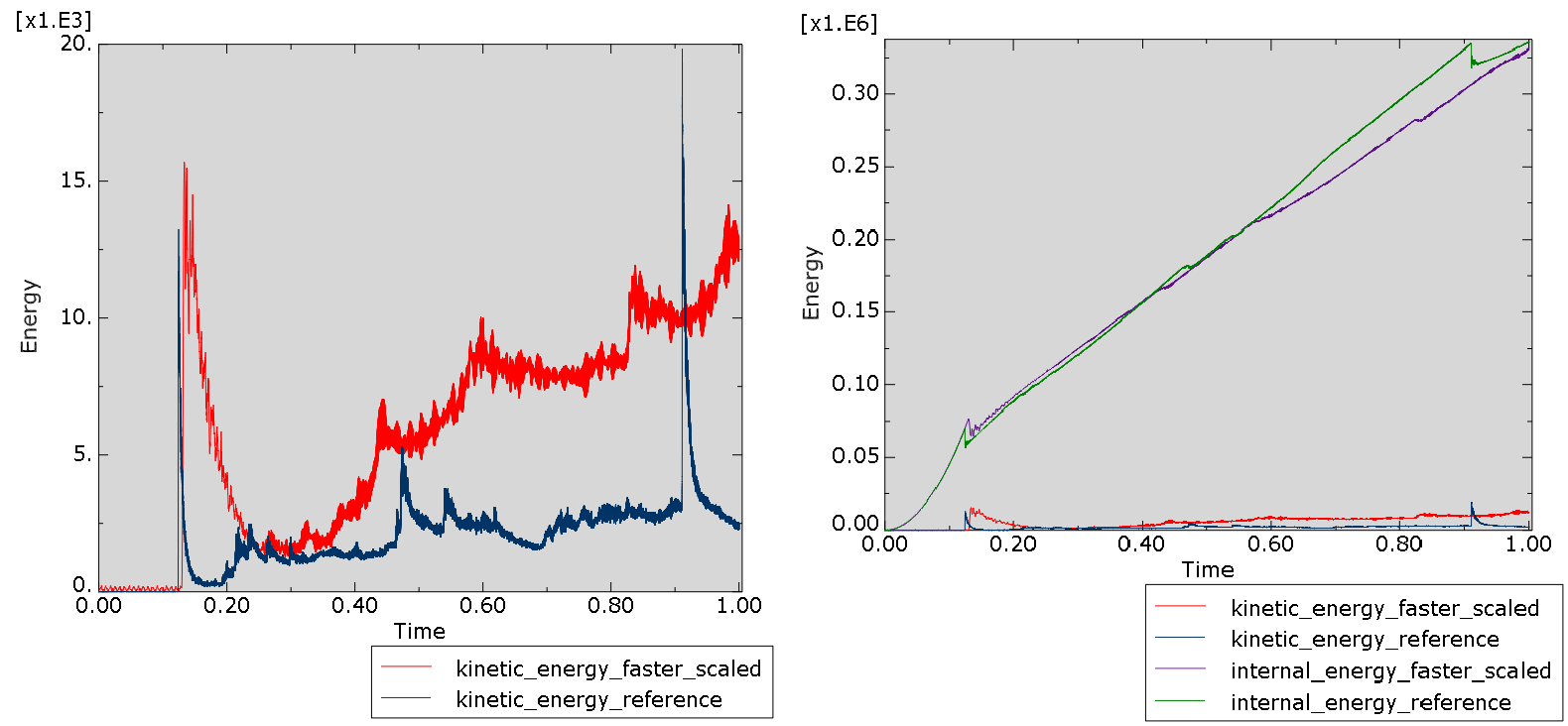
Figure 5: Kinetic energy for slower and faster load application, without (left) and with (right) internal energy for comparison. Time is scaled for the faster load application case, to the applied displacement matches. The kinetic energy is larger when the load is applied faster. Before buckling, the difference is barely noticeable.

Conclusion

Abaqus/Standard and Abaqus/Explicit each have their pros and cons. Abaqus/Standard is very good at solving linear to mildy non-linear problems with large time scales quickly, while it can slow down or possibly not find a solution at all for extremely non-linear problems. Abaqus/Explicit, on the other hand, excels at extremely non-linear problems with small time scales. For problems with a large time scale simulation times can be prohibitively long. The more noisy solutions can also be an issue.

The simple example of the bending cylinder confirmed this: before the onset of buckling Abaqus/Standard found a solution quickly. This was a static solution, and the reaction force curve was nice and smooth. After the onset of buckling, Abaqus/Standard could not find a solution any more. In Abaqus/Explicit, on the other hand, the analysis continued without difficulties. The reaction forces were noisy in this case. By scaling the simulated time in the Explicit analysis the simulation time could be reduced. This also led to more dynamic effects, as observed by a more noisy reaction force and higher kinetic energy.