Modelling Rubber Materials With Abaqus

In this blog we will focus on the capabilities of Simulia Abaqus to assist in modelling rubber like materials.

Rubber materials such as thermoplastics are largely used in the industry; to list some of the areas where these materials can be found we can mention tyre industry, consumer pack goods, medical or sealing solutions but rubbers are also present in many others engineering fields. Today I will dedicate the next lines to the sealing market due to its beneficial ratio between ease to explain-build up a model and the high end capabilities that Abaqus can provide.

Using simulations in the design phases of sealing solutions is becoming a necessary step that can help identifying and gaining a better understanding of the behavior of the product. Well established companies in the sealing field like Trelleborg, Parker, Eriks, Lagersmit, have been extensible using Simulia’s Abaqus Finite Element Analysis (FEA) to aid in their development/test stages. In many cases due to its complex geometries and material properties it is not clear how the product performs until a practical test is conducted. Even then, from experiments only limited information can be obtained whereas from numerical simulations hundreds of variables can be studied and the behaviour of prototypes can be estimated without incurring in large costs.

Setting up an Accurate Material Model

Hyperelasticity

One of the most important things in any FEA is to have a good description of the material. In this case rubbers are hyperelastic materials, they can bear very large deformations without suffering plastic strains. Abaqus has several hyperplastic material models that can capture the response of most commercial rubbers. The parameters that describe the models can be easily fit to experimental data. For example, you can conduct a tensile test and then use that information as input in Abaqus. Internally, the parameters will be automatically obtained by numerical fitting. Abaqus supports four kind of experiments: uniaxial tension, equibiaxial tension, shear and volumetric test.

Viscoelasticity

Another very important effect in rubber materials is called viscoelasticity. In this case the material does not behave in the same manner over time but is history dependent; polymer chains can slide over each other as time increases. In this way two very important concepts should be mentioned: creep and stress relaxation. In the first case a constant load is applied and the deformation increases over time until the equilibrium is reached. In the second case a deformation is applied and the resultant reaction force drops over time until, again, the equilibrium is reached. Like for the hyperelastic models Abaqus also provides models to capture these important phenomena and thus, account for linear and nonlinear viscoelasticity. The user has to fit these models to experimental data. In this case shear and volumetric test are supported (both for creep and for stress relaxation).

Example: Mechanical Seal

Model description
In the following example a rubber material will be used to model a sealing solution. The example will provide a better understanding of the previously mentioned behaviour and will also introduce the concept of pressure penetration, particularly interesting to simulate the effects of a fluid pushing and trying to move forward without modelling the fluid itself.

The example consists of a seal with an axisymmetric shape. The seal, as shown in Figure 1, has three lips that extend inwards to provide flexibility to adjust and fit to the inner pipe. The three lips create three faces that will resist the pressurized fluid that is intended to remain on one side of the system.

A Neo Hookean hyperelastic model has been used in combination with a viscoelastic model fitted to experimental shear relaxation data. 
 
Figure 1: Axisymmetric geometry of the three-lip seal.

Simulation

Step 1: Fitting the seal: The seal is mounted on the rigid pipe by an axial displacement, Figure 2. For visualization purposes a only a 45 degree sector of the axisymmetric system is shown. After the seal has been adjusted to the pipe large stresses have been developed in the rubber material, Figure 3. This is expected because the outer diameter of the pipe is larger than the inner diameter of the seal so that a press-fit connection can be guaranteed.
 

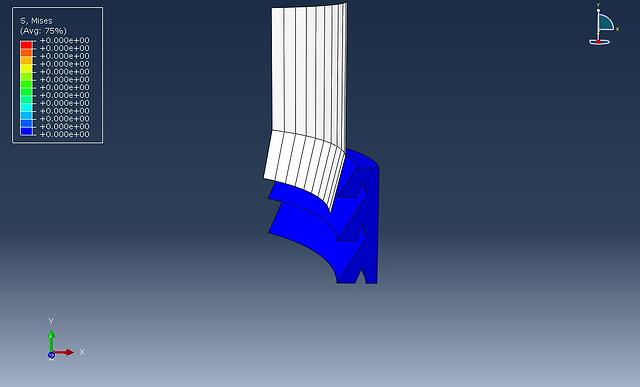
Figure 2: Initial position of the pipe and seal before assembling procedure. The pipe will displace axially downwards.
 

Figure 3: Stresses developed in the seal after mounted in the pipe.

Step 2: Stress Relaxation: In the second step the time is increased and the effects of viscoelasticity can be observed. Due to this time dependent material properties the stresses relax almost four times, Figure 4. At the end of Step 1 the maximum stress was 214.4 MPa and after relaxation the maximum stress drops to 58.9 MPa.
 

Figure 4: Stress relaxation in the seal after 50 seconds.

Step 3: Pressure Penetration: In the third step an internal pressure of 5 MPa was simulated acting normal to the faces of the pipe and the top lip. Such pressure was enough to separate the first lip (top) from the pipe thus penetrating to the second level (second lip). However, such pressure was not enough to open the second lip, Figure 5. Therefore, with thess boundary conditions the system can be considered leak free. 

Figure 5: Pressure penetration; Top: geometry after stress relaxation. Bottom: pressure exerted on the lip face while the time increases. 5 MPa internal pressure can penetrate up to the second lip but cannot go any further.

With this kind of simulations you can tune the internal pressure in order to determine which is the pressure that opens the first seal and penetrates to the second. The advantage of pressure penetration against conventional internal pressure is that with the latter you can only specify upfront where the pressure acts and if it is enough to open the first seal, but it will stop there, it will not penetrate to the second chamber. On the other hand, pressure penetration simulates that once the first seal lip has failed then the fluid can penetrate further. Thus, by using pressure penetration you can monitor whether the pressure would still be enough to open the second lip or the process will stop there making the sealing solution still leak free.
Finally, I would like to make emphasis on the importance of considering viscoelasticity for rubber like materials. Figure 6 shows the radial reaction force on the seal as a consequence fitting it to the pipe. The force created in this step reaches a maximum of nearly 110 N. However, due to viscoelastic effects this force will drop after 50 s to a value below 40 N when a near equilibrium condition has been reached. The effect can be summarized on the seal becoming loose and therefore, we can predict that during the pressure penetration step a relatively low internal pressure can be enough to open the first lip.

Importance of Considering Viscoelastic Effect

Importantly, if viscoelastic effects would not have been considered then obviously the reaction force would not have dropped and the same internal pressure used for the pressure penetration step would not have been enough to make the first lip to fail, see blue line in Figure 7 and Figure 8.
 

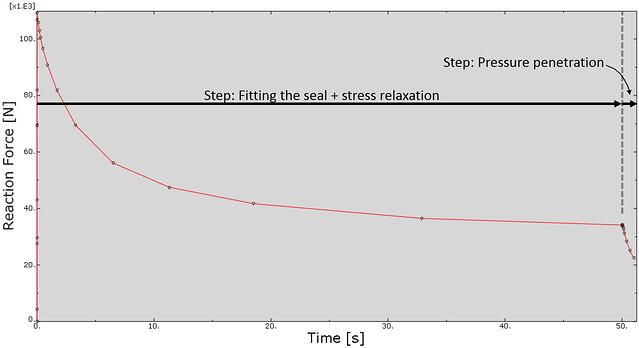
Figure 6: Radial reaction force throughout the entire simulation. Step 1 & 2: Fitting the seal + Stress relaxation, Step 3: Pressure penetration.
 

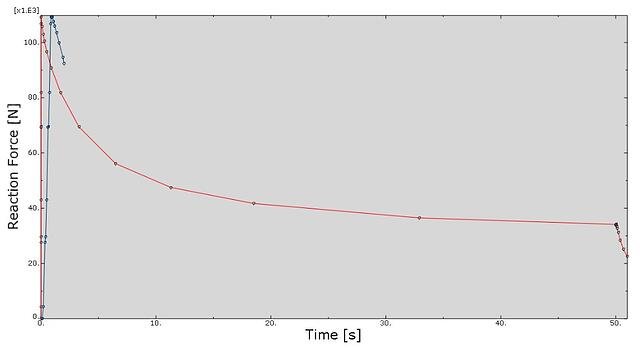
Figure 7: Radial reaction force as mentioned in Figure 6 along with radial reaction force (blue) when  no viscoelasticity is considered, and therefore no stress relaxation step has been included.
 

Figure 8: Pressure penetration when no viscoelasticity in considered. In this case the pressure will not make the first lip to fail.

Summary

• Simulia’s Abaqus FEA can accurately predict the behaviour of rubber like materials for which it includes several material models for hyperelasticity and viscoelasticity.
• The user can fit such models to experimental data automatically in Abaqus. Experiments such as uniaxial tension, equibiaxial tension, shear and volumetric are supported.
• Pressure penetration is a simple and at the same time very powerful capability to evaluate the leak free behaviour of mechanical seals.
• It was shown that not accounting for viscoelasticity can have dramatic effects on the predicted results.

Are you interested in knowing more about Abaqus functionality to model rubber like materials?
Join our upcoming workshop > Accurately predict non-linear behavior of Plastics & Rubbers with Abaqus FEA.